Pada kali ini kita akan belajar tentang sistem pertidaksamaan linear dua variabel. Hal yang membedakan sistem persamaan linear dan sistem pertidaksamaan linear dua variabel adalah tanda/relasi yang digunakan. Jika pada persamaan linear tanda yang digunakan adalah tanda "=", maka pada pertidaksamaan linear tanda yang digunakan adalah tanda-tanda ketaksamaan, seperti: >, <, ≥, dan ≤.
Tanda ketaksamaan tersebut muncul karena terdapat batasan yang diberikan permasalahan yang kita modelkan. Contohnya seperti permasalahan berikut.

Pada ilustrasi di atas, terlihat bahwa terdapat kendala yang membatasi jumlah kursi yang dihasilkan, yaitu jumlah semen dan pasir yang tersedia. Kendala inilah yang kita nyatakan dalam pertidaksamaan linear.
Sistem pertidaksamaan linear lengkap yang dapat kita modelkan dari permasalahan di atas adalah sebagai berikut.
dengan adalah konstanta.
Banyaknya pertidaksamaan linear yang terdapat pada sistem pertidaksamaan linear dua varibel tidak terbatas seperti pada contoh di atas. Pertidaksamaan linear yang diperoleh bisa saja lebih banyak atau lebih sedikit, tergantung kendala yang diketahui pada soal/permasalahan. Kalian akan mempelajari cara memodelkan sistem pertidaksamaan linear dua variabel pada topik selanjutnya. Jangan dilewatkan ya.
Berdasarkan penjelasan di atas, dapat disimpulkan bahwa,

Selanjutnya kita akan mempelajari cara menentukan penyelesaian dari sistem pertidaksamaan linear dua variabel.
Bagaimana Menentukan Daerah Penyelesaian dari Sistem Pertidaksamaan Linear Dua Variabel?
Salah satu cara menentukan daerah penyelesaian dari sistem pertidaksamaan linear adalah dengan menggunakan grafik. Namun, sebelum kita memulai pembahasan mengenai penyelesaian dari sistem pertidaksamaan linear dua variabel, mari kita ingat kembali materi tentang persamaan linear dua variabel.
Suatu persamaan linear dua variabel berbentuk , dapat digambarkan sebagai sebuah garis pada bidang Cartesius.
Misalkan terdapat suatu persamaan yang akan digambarkan pada bidang koordinat Cartesius. Persamaan garis tersebut dapat digambarkan dengan menentukan tiitk potong garis tersebut dengan sumbu x dan sumbu y.
Titik potong dengan sumbu x:
Koordinat titik potong garis dengan sumbu x yaitu (0,4) .
Titik potong dengan sumbu y:
Koordinat titik potong garis dengan sumbu y yaitu (4,0).
Hubungkan kedua titik potong tersebut, maka garis tersebut mewakili persamaan , seperti gambar di bawah ini.
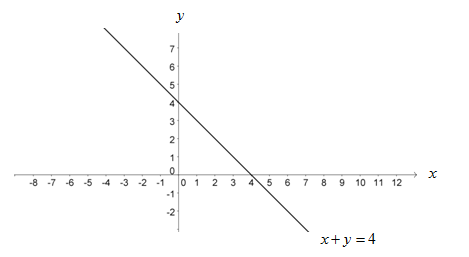
Garis tersebut membagi bidang Cartesius menjadi 2 bagian, yaitu di sebelah kiri garis dan di sebelah kanan garis.
Misalkan kita hendak menentukan daerah penyelesaian dari pertidaksamaan
Untuk menentukan daerah yang memenuhi pertidaksamaan tersebut, kita ambil sebuah titik uji, misalkan titik (0,0).
Untuk menentukan daerah yang memenuhi pertidaksamaan tersebut, kita ambil sebuah titik uji, misalkan titik (0,0).
Jika kita substitusikan titik (0,0) pada pertidaksamaan , maka kita peroleh,
Oleh karena titik (0,0) memenuhi pertidaksamaan , berarti titik (0,0) berada pada daerah penyelesaian dari
Daerah adalah daerah yang diarsir pada gambar berikut ini.
Daerah adalah daerah yang diarsir pada gambar berikut ini.
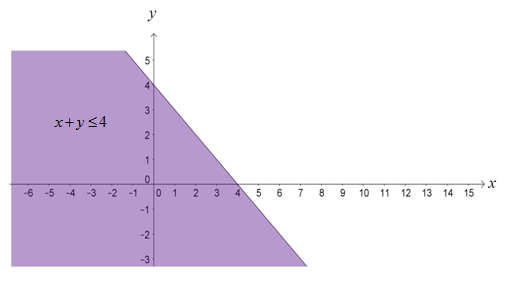
Dengan cara yang sama, kita dapat menentukan daerah penyelesaian dari pertidaksamaan
Oleh karena titik (0,0) tidak memenuhi pertidaksamaan , maka daerah penyelesaian dari adalah daerah di sebelah kanan garis .
Daerah adalah daerah yang diarsir pada gambar berikut ini.
Oleh karena titik (0,0) tidak memenuhi pertidaksamaan , maka daerah penyelesaian dari adalah daerah di sebelah kanan garis .
Daerah adalah daerah yang diarsir pada gambar berikut ini.
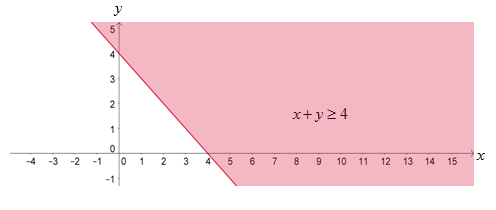
Agar lebih mudah menentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel, gunakan trik pada tabel berikut ini.

Catatan:
Apabila tanda ketaksamaannya adalah atau , maka garisnya adalah garis penuh (garis termasuk dalam daerah penyelesaian).
Apabila tanda ketaksamaannya adalah > atau <, maka garisnya adalah garis putus-putus (garis tidak termasuk dalam daerah penyelesaian).
Berdasarkan uraian di atas, dapat kita simpulkan langkah-langkah dalam menentukan penyelesaian dari sistem pertidaksamaan linear dua variabel adalah sebagai berikut.
- Ubah setiap pertidaksamaan linear menjadi persamaan garis.
- Gambarkan grafik dari setiap persamaan garis dengan menghubungkan titik potongnya terhadap sumbu-x dan sumbu-y. Jika pertidaksamaan memuat tanda > atau <, maka gambarkan garisnya dengan garis putus-putus.
- Ambil titik uji untuk menentukan daerah yang memenuhi setiap pertidaksamaan dan berikan arsiran pada daerah tersebut.
- Tentukan daerah penyelesaian dari sistem pertidaksamaan linear, yaitu daerah yang merupakan irisan dari daerah-daerah yang memenuhi setiap pertidaksamaan linear yang diberikan.
Adakalanya, dalam soal mengenai sistem pertidaksamaan linear dua variabel, diketahui grafik tanpa persamaan garisnya. Untuk itu, kalian harus mengingat kembali cara menentukan persamaan garis berdasarkan 2 titik yang diketahui, yaitu sebagai berikut.
MIsalkan garis g melalui dua buah titik yaitu , maka persamaan garis gdapat ditentukan dengan rumus:
✎Contoh Soal
Tentukan daerah penyelesaian dari sistem pertidaksamaan linear berikut ini.
✍ Penyelesaian:
Langkah-langkah penyelesaian :
1). Ubah pertidaksamaan menjadi persamaan garis.
2). Gambar grafik garis , , dan .
Garis


Garis


Garis merupakan garis yang berimpit dengan sumbu y.
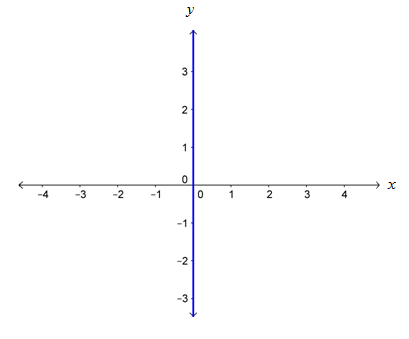
3). Ambil titik uji untuk menentukan daerah yang memenuhi setiap pertidaksamaan dan berikan arsiran.
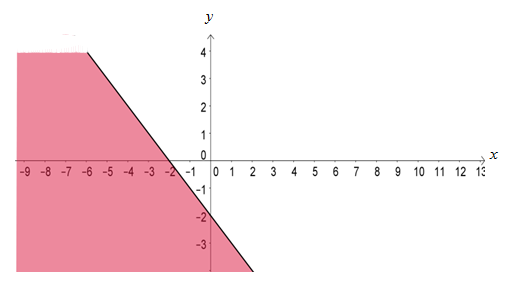
Daerah penyelesaian dari
Jika diambil titik uji (0,0), maka diperoleh 0 + 0 = 0 > -2. Ini berarti titik O(0,0) tidak berada pada daerah penyelesaian pertidaksamaan .
Jadi daerah penyelesaian dari pertidaksaman berada di sebelah kiri atau di bawah garis
Oleh karena tanda ketaksamaannya adalah ≤, maka garis termasuk pada daerah penyelesaian (garis digambar penuh).
Jika diambil titik uji (0,0), maka diperoleh 0 + 0 = 0 > -2. Ini berarti titik O(0,0) tidak berada pada daerah penyelesaian pertidaksamaan .
Jadi daerah penyelesaian dari pertidaksaman berada di sebelah kiri atau di bawah garis
Oleh karena tanda ketaksamaannya adalah ≤, maka garis termasuk pada daerah penyelesaian (garis digambar penuh).
Daerah penyelesaian dari :
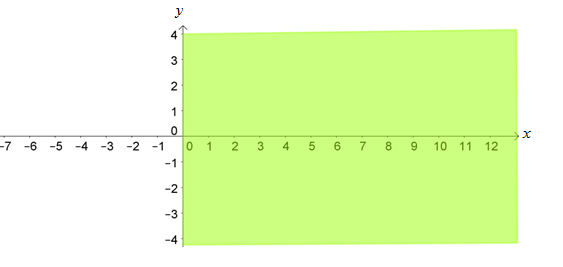
Jika diambil titik uji (0,0), maka diperoleh 0 + 0 = 0 > -7. Ini berarti titik (0,0) berada di daerah penyelesaian pertidaksamaan
Jadi daerah penyelesaian dari pertidaksamaan berada di sebelah kiri garis
Jika diambil titik uji (0,0), maka diperoleh 0 + 0 = 0 > -7. Ini berarti titik (0,0) berada di daerah penyelesaian pertidaksamaan
Jadi daerah penyelesaian dari pertidaksamaan berada di sebelah kiri garis

Daerah penyelesaian dari :
4). Menentukan daerah penyelesaian dari sistem pertidaksamaan yaitu irisan daerah penyelesaian dari setiap pertidaksamaan.
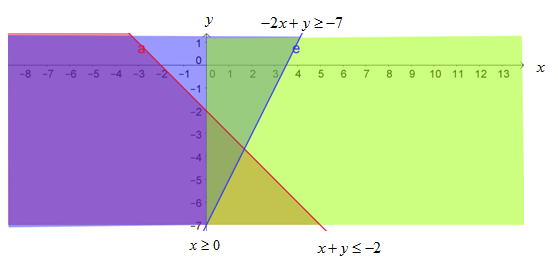
Berdasarkan gambar di atas terlihat bahwa terdapat daerah yang dilalui oleh 3 arsiran dengan warna yang berbeda (biru, merah muda, dan hijau). Daerah irisan dari ketiga daerah penyelesaian itulah yang merupakan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel pada contoh di atas.
Agar lebih jelas, daerah penyelesaian sistem pertidaksamaan tersebut disajikan pada gambar berikut ini.
Agar lebih jelas, daerah penyelesaian sistem pertidaksamaan tersebut disajikan pada gambar berikut ini.
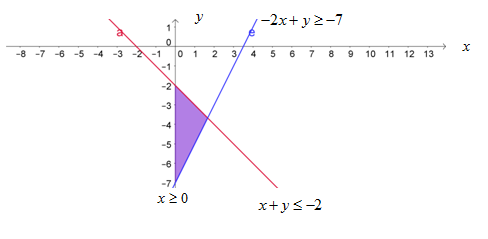

0 komentar